For more examples see the SimuLase manual and our various publications.

Gain/Absorption


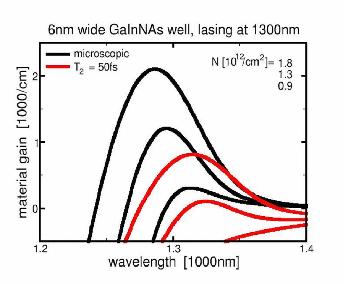
Black lines: Results of the fully microscopic model for the GaInNAs-structure shown in the examples. Red lines: Results for the same densities as in the full model, but with a model that does not calculate the scattering microscopically but uses a dephasing time to simulate the line broadening. Otherwise, this model includes all effects (bandgap renormalization, Coulomb enhancement, band nonparabolicities,...) the full model does.

The above example demonstrates the errors arisong from using a dephasing time or a line-broadening instead of calculating the underlying electron-electron and electron-phonn scattering processes explicitly. Even if experimental data is known and a decent fit to it can be found for one carrier density, the fit will fail for higher and lower densities. Also, spectral positions and the gain amplitude to carrier density relation will be significantly wrong. This approach requires the previous knowledge of the experimental result for any decent agreement. Thus, it has no predictive capabilities but relies on fitting.

These strong general shortcomings are inherent to all attempts using broadenings, no matter how 'sophisticated' they are. Although some methods (like 'non-Markovian gain models') avoid e.g. the non-physical absorption tail energetically below the gain that simple Lorentzian lineshape broadening produces, however this is merely cosmetics. The underlying microscopic scatterings are strongly dependent not only on the carrier density but also the temperature and spectral position. They introduce mixings of the complex microscopic polarisations that lead to spectral lineshape modifications, amplitude modifications and energy renormalisations that cannot be captured through broadenings of individual transitions.

The error in the density-amplitude relation would make any attempts to calculate input-output currents as demonstrated in Close Loop Design impossible. Since the loss currents scale more than linearly with the carrier density, errors in the threshold density of several tens of percents would lead to even bigger errors in the loss currents.
For shortcomings due to neglect of the conduction band nonparabolicity or the Coulomb induced intersubband coupling see e.g. Ref.[10].



Spontaneous Emission (Photo Luminescence)

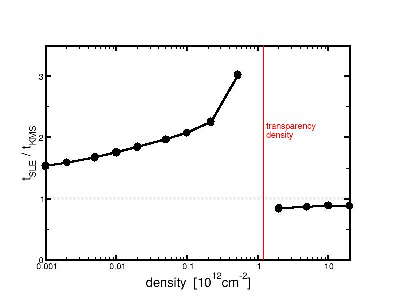
Ratio between radiative carrier lifetimes as calculated with the semiconductor luminescence equations and those obtained when using the KMS-relation. Here, for the structre investigated in the example for the Closed Loop Design.

The above picture demonstrates the shortcomings of the Kubo-Martin-Schwinger (KMS) relation which calculates the spontaneous emission by a simple integral conversion of the gain/absorption spectra. The KMS relation is strictly valid only in the absence of any broadenings. However, the correct calculation of the absorption/gain requires the inclusion of the homogeneous bradening due to electron-electron and electron-phonon scattering. The KMS-forlmula has a pole at the position of the chemical potential. If this is energetically in the low energy tail of the absorption it artificially enhances the spontaneous emission and, thus, leads to an underestimation of the radiative carrier lifetime which is given by the inverse of the integral over the spontaneous emission. Thus, the KMS-results can be off by a factor of two or more.
This error becomes most dramatic when the chemical potential is just below the bandgap, i.e. for densities just below transparency. For higher densities the chemical potential is at the position of the transparency point where absorption/gain is zero. This prevents an artificial pole in the results. However, as shown in the example above, since the KMS neglects the excitonic correlations that are included in the luminescence equations, the results of the KMS are wrong there too and so are in general the lineshapes calculated with KMS.


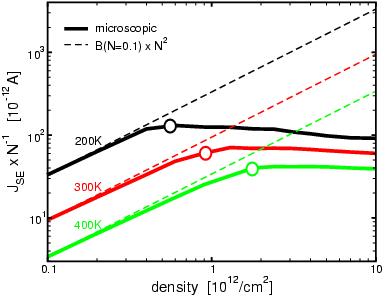
Loss currents due to radiative recombination, J_SE, divided by the carrier density. Bold lines: as calculated with the semiconductor luminescence equations. Thin lines: using the power law, J_SE=BN². Here, the coefficient, B, was derived by fitting the power law to the low density result of the microscopic calculation at N=10¹¹/cm². The open signs mark the threshold carrier densities. Here for the GaInNAs/GaAs-structure investigated in the examples.

An often used, even simpler approach to calculating the carrier lifetimes due to spontaneous emission than using KMS is to use a power law, J_SE=BN², to describe them. This power law holds approximately in the limit of very low carrier densities where the carrier distributions can be described by Boltzmann distributions. However, it fails for densities where phase space filling becomes significant, i.e. near transparency and above. Even if as in the example above the exact value for B is known from the low density result, the results of the power law are off by about a factor of two near threshold and the error can easily reach one order of magnitude.
It can be shown analytically that for very high densities the density dependence of the radiative losses changes from quadratically to only linear. This can be seen in the picture above where J_SE/N as calculated microscopically approaches a constant value for high densities.

For more details see e.g. Refs.[28] and [29].




Auger Recombination Processes


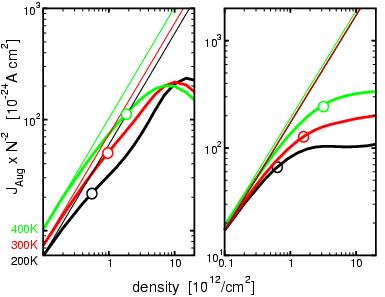
Loss currents due to Auger recombination processes, J_aug, divided by the square of the carrier density. Bold lines: calculated microscopically. Thin lines: using the power law, J_aug=CN³. Here, the coefficient, C, was derived by fitting the power law to the low density result of the microscopic calculation at N=10¹¹cm². The open signs mark the threshold carrier densities. Left: for the GaInNAs/GaAs-structure investigated in the examples. Right: for the InGaAsP/InP-structure operating at 1.5µm.

Auger recombination losses are often described using a simple power law for the loss current, J_aug=CN³. Using some rough approximations, this density dependence can be shown analytically to be correct for low densities where the carrier distributions can be described by Maxwell-Boltzmann distributions. However, for in the regime important for laser operation, i.e. near transparency and above, the density dependence becomes less than cubic. as shown for two examples in the picture above, here, the density dependence can become only quadratically (which would yield horizontal lines in the way the data is plotted in the picture) or even less. Even if as here the correct low density value for C is known from the microscopic calculation, the results of the power law are off by a factor of two ore more near threshold. At higher densities, the power law can lead to an error of one order of magnitude or more.


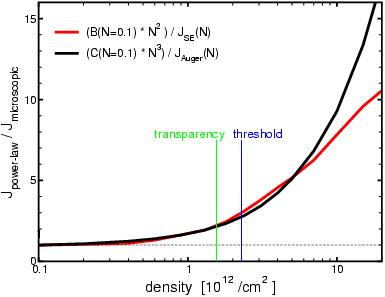
Ratios between microscopically calculated loss currents and loss currents when using power laws with the coefficients B and C fitted to the microscopic results at low densities. Red: loss currents due to spontaneous emission. Black: loss currents dur to Auger processes. Results for the InGaAsP/InP-structure operating at 1.5µm.

The above picture demonstrates as the two previous pictures the shortcomings of the power laws, J_SE=BN² and J_aug=CN³. Near threshold the power laws are off by a factor of three. For higher densities the error can easily reach one order of magnitude or more.

For more details see e.g. Refs.[28] and [29].